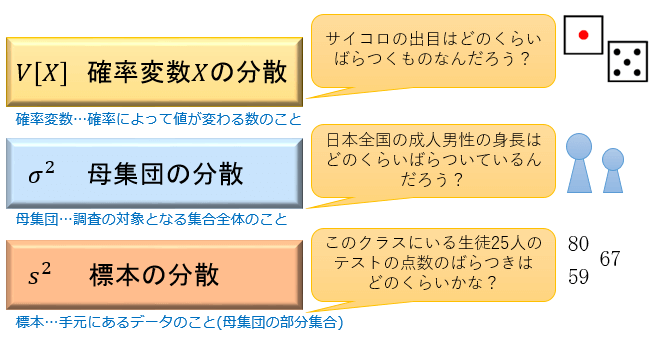
これは,普通のサイコロの期待値35の 2倍である。 17 期待値の性質 x,yが確率変数のとき,Ex y Ex Ey()()() 二つのサイコロを同時に振って出た目を足した値について考える。 二つのサイコロの出目の和は2と12の間になり,その中心の値 (期待値)は7である。確率変数と確率分布 ・標本空間(sample space):実験や観察のあらゆる可能な結果を表す点の集合 ・標本点(sample point):標本空間中の各点で、それぞれ1つの可能な結果や事象 ・各標本点には、確率が付与される ・確率変数(random variable):標本空間の標本点に対応して値が決まる変数サイコロの目の期待値と分散・標準偏差 1 2 3 4 5 6 合計 1/6 1/6 (1/6)u6 1 u(1 /6) 2u(1/6) 3u(1/6) 4u(1/6) 5u(1/6) 6u(1/6) 21/6 35 (1 35)2u(1/6) (2 35)2u(1/6) (3 35)2u(1/6) (4 35)2u(1/6) (5 35)2u(1/6) (6 35)2u(1/6) 175u(1/6) 292 ak pk akpk ak pk ( P)2 ¹ >8P E>X@ ( S>8 3
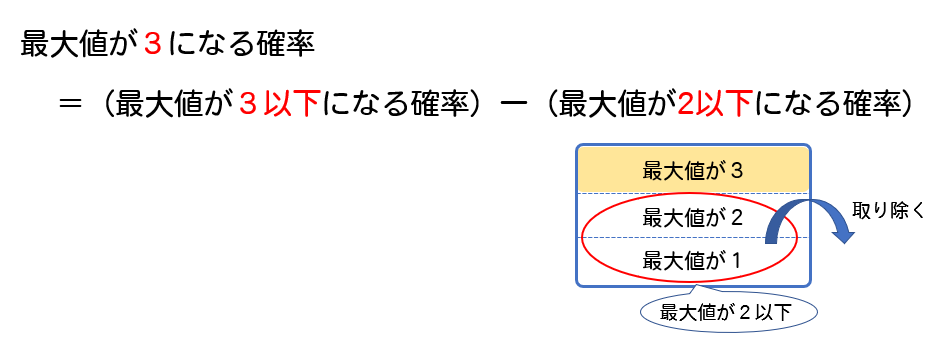
数学a サイコロの最大値が5 最小値が2になる確率はどうやって考える 数スタ
サイコロ 3つ 和 期待値
サイコロ 3つ 和 期待値-3 = 276 / 15 = 184 さらに,次はじデータの確率分布表です。 data 1 2 3 4 5 和 x 1 5 3 4 6 19 p 2/15 3/15 5/15 4/15 1/15 113 期待値(Expectation) 確率変数X, 実数上で定義された関数f に対して ∑!2 jf(X(!))jP(f!g) < 1;



二項分布とは 期待値 分散の計算や 正規分布による近似 受験辞典
確率変数の期待値(1) 期待値:確率変数の平均的な値 離散型確率変数:𝐸 =𝑝1𝑥1𝑝2𝑥2⋯ 例:x = (1つのサイコロを投げた時の出目) 𝐸 =1/6×11/6×21/6×3 1/6×41/6×51/6×6 =7/2 1つのサイコロを60,000回投げたとする。およそ10,000二つのサイコロを同時に振って出た目を足した値について考える。 二つのサイコロの出目の和は2と12の間になり,その中心の値 (期待値)は7である。この値は,一つだけサイコロを振ったときの 期待値35を2つ足し算したときと同じである。 和May 11, · 6個のサイコロを同時に投げて、その目の和を求める行為を繰り返す場合、サイコロの目の和の分散は? ① 35 ② 35 / 2 ③ 35 / 3 ④ どれでもない 正解は「② 35 / 2」 1個のサイコロを投げた場合のサイコロの目の平均は3.5。 同様に分散は、 { ( 1 35 )^2 ( 6 35 )^2 } / 6 = 35 / 12 1つ1つの
式(1)を確認するシミュレーションプログラムを作成した。このプログラムを実行すると図1のようにサイコロ投げの回数(図1では i で表されている)が大きくなるにつれて平均値 mean は期待値 35 に近づくことが確認できる。サイコロの出目の期待値と分散 3 12 35 12 35 35 2 7 v x v x e x 標準偏差 分散 期待値 0 1234 567 000 010 0 030 x p e x 35絶対収束 を満たすときf(X) は可積分であるといい Ef(X) ∑!2 f(X(!))P(f!g) をf(X) の期待値とよぶまた, f(X) が可積分, A が事象であるとき Ef(X);A ∑!2A f(X(!))P(f!g) と記す 例) 1) f(x) = x のとき, 期待値EX は
3つのサイコロの出る目の和の確率 3つのサイコロa,b,cを振ったとき,目の和が10となる確率を求めよ. また,この試行の期待値はいくつか? 3つのサイコロの出る目の和の確率分布 3つのサイコロa,b,cを振って,出た目の和を求める試行を1000回行った. この実験結果(相対度数)を棒グラフに表現せよ. また,そのグラフに確率(理論値)を線グラフとして追加Jul 29, · 期待値 サイコロ 3回 2907, por 中小企業 生産性向上 ガイドライン 大学の確率問題です。 この問題を教えてください。 期待値の問題です。 さいころを繰り返し投げて、出た目の和だけの金額 (単 位は円)をもらう。 さいころは何回投げてもよいが、目の和が11以上になると失格となって全然もらえないことになる サイコロを1回ふり、1が出たら10円、2が出たら公式3は x x x と y y y が無相関でなくても成り立つ 素晴らしい公式です。→和の期待値は期待値の和。一方,公式4は x x x と y y y が無相関なときのみに成立する公式です。



サイコロの目の平均 分散 標準偏差



Excel De Asobo Section 6
Apr 19, 17 · r言語はシミュレーターとして使うことができます。例えば、コインを100回投げたときに表が何枚出るのかを、実際にやってみるのは大変です。また、サイコロを1000回ふって、実際にどの目も(約)6分の1の確率で出ることを体感して確認しようとしたらなかなか骨の折れる作業になるMay 05, 18 · 公式:期待値 ・和の期待値=期待値の和 (期待値の線形性の性質) EX Y = EX EY ・定数倍の期待値=期待値の定数倍(期待値の線形性の性質) EaX = aEX (aは定数) ・独立な確率変数の積の期待値=期待値の積 XとYが独立な確率変数であるとき、積XYの期待値はそれぞれの期待値の積に等しい。 EXY = EXEY ・定数の期待値=定数May 15, · もし、期待値を最大化したいなら、 投げないほうがよいでしょう。 3回目を投げた場合の期待値は、17/3円 で 6円よりも小さいです。 もし、もらい得る金額の最大値を最大化したいなら、 そこまでの目の和が 10未満であるうちは



確率の期待値とは 求め方と高校の新課程での注意点




期待値と分散に関する公式一覧 高校数学の美しい物語
サイコロを1回ふり、1が出たら10円、2が出たら円、3が出たら40円、4が出たら60円、5が出たら80円、6が出たら0円獲得出来るものとする。 獲得賞金の期待値はいくらか? (手順1) まず 事象( 1,2,3,4,5,6 )と それぞれの賞金( 10, , 40, 60, 80, 0 )を書き込みます。 (手順2) 次に確率を計算しますが、この問題は計算するまでもなく、全ての場合の確率が 1/6=14/3 答え 14/3万円。 プログラムを組んでシミュレーションした結果回の実験で4.665となりました。 補足 1回であれば、期待値は3.5万円。 1,2,3のとき次のサイコロを振る作戦のときの期待値は37/8万円。期待値の和=和の期待値 上記の公式は 「和の期待値は期待値の和に等しい」 ことを表しています。 期待値のこのような性質を「期待値の線形性」と言います。 (線形性についてのより詳しい説明は 高校数学における線形性の8つの例 参照) 期待値の線形性は X X X と Y Y Y が独立でなくてもどんな場合にも成立する強力な公式です。




中心極限定理の例とメリットをわかりやすく解説 Avilen Ai Trend
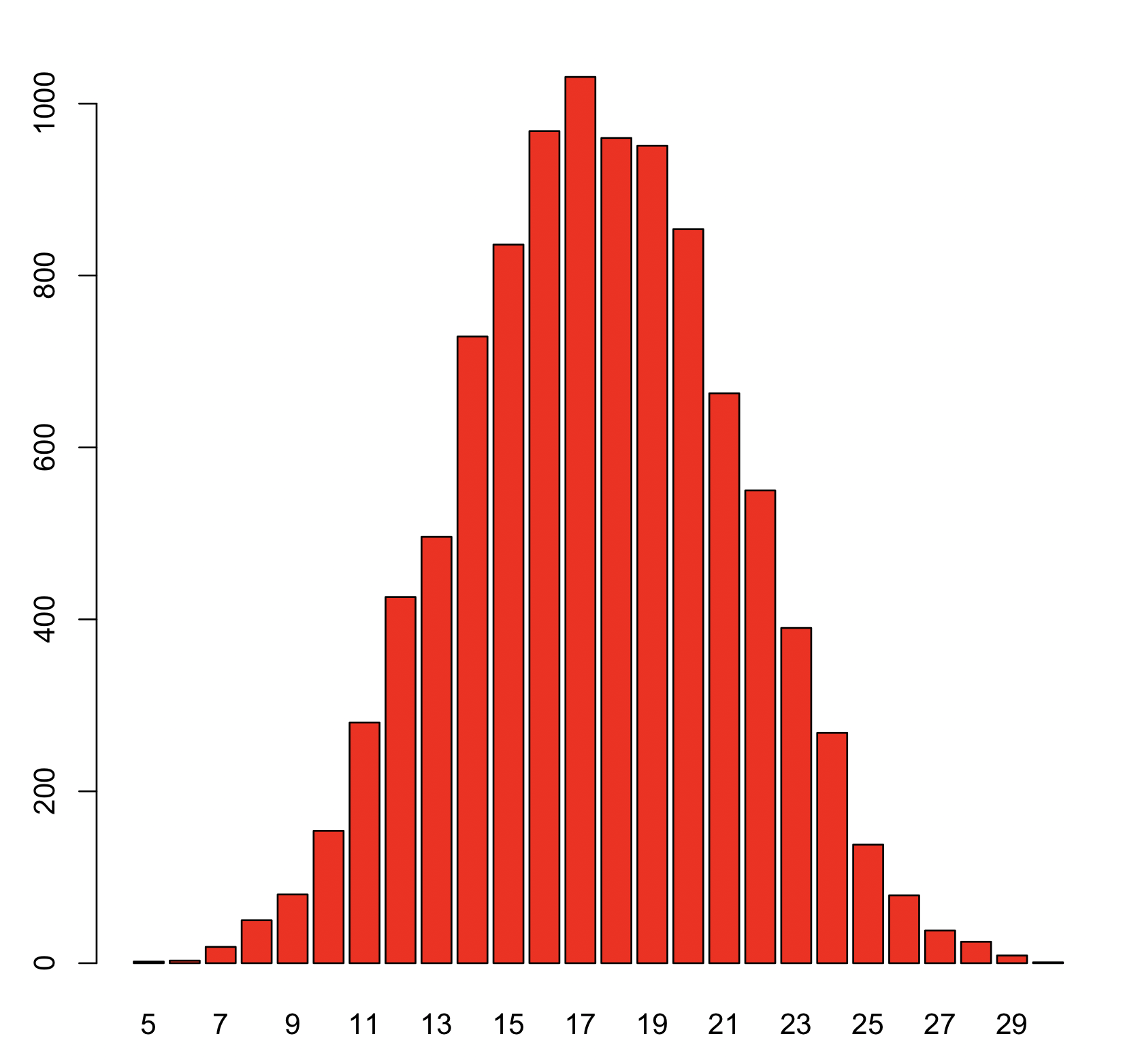



Rでサイコロの和のシミュレートをしてグラフ化する Avilen Ai Trend
Sep 10, 07 · まず、簡単に求められる「期待値の二乗:e(x)^2」を求めます。 サイコロを2個振った時の期待値は、問題1と同様に、サイコロ1個振った時の期待値の2倍、 e(x)=7/2×2=7になります。 したがって、 e(x)^2=7^2=49 次に、「二乗の期待値:e(x^2)」です。(3)1,2,3,4,5,6の目がすべて出る。 (東海大一教養) サイコロ3個を同時にふるとき,出た目の数の和が12になる確率を求めよ。(立教大一理) 1個のサイコロを2回投げるとき,1回目に出る目をαとし,2回目に出る目をあとする。実際,赤玉が3個と白玉が2個あるときに,3個同時に取り出す場合でも,赤玉の個数の期待値と白玉の個数の期待値は, =32 が成り立っている.(ただし,この場合は, =3 )



期待値とは 計算公式と求め方 確率変数 確率分布の意味も 受験辞典




Ppt 確率と統計 確率2回目 Powerpoint Presentation Free Download Id
二つのサイコロAとBを同時に投げたときの出目の和 5 0 1 2 3 4 5 6 7 0 0 0 0 1 0 0 2 0 0 3 0 x p 0 1 2 3 4 5 6 7 0 0 0 0 1 0 0 2 0 0 3 0 xここで期待値の和を問う過去問題を紹介しよう. 演習 18 04北大前期理系解答18 ある人がサイコロを振る試行によって,部屋a,bを移動する サイコロの目の数が1,3のときに限り部屋を移る. また各試行の結果,部屋aに居る場合はその人の持ち点に1点を3 期待値とは、各データと期待値との差の2 乗和を最小にする値である。 任意の値c を使って X (xi ¡E(X))2 < X (xi ¡c)2 (6) が成り立つ。右辺のカッコ内でE(X) を引いて、足して、も答えは変 わらない。



サイコロの期待値は 3 5 アルファ ファイナンシャルプランナーズ



サイコロを2つまたは3つ以上振る確率の求め方と重複試行
また,この試行の期待値はいくつか? 2つのサイコロの出る目の和の確率分布 2つのサイコロa,bを振って,出た目の和を求める試行を1000回行った. この実験結果(相対度数)を棒グラフに表現せよ. また,そのグラフに確率(理論値)を線グラフとして1の目が出る回数の期待値は、 回 ということになります。6つの目が均等に出れば、3回振れば05回の割合で1が出るということになります。 なお、期待値を計算するときは、上の計算のように確率を求めるときに約分しないでおくのがコツです。Fig 2 二つのサイコロを振ったときに出る目の和 S 2 の確率分布 三つのサイコロを振って出る目の和 S 3 は,3 から 18 までの値をとり,確率分布は Fig 3 のようになります。




2 4 135 Descubre Como Resolverlo En Qanda




サイコロ Wikiwand
サイコロの目の出る確率 全種類のカードを集めるには 大相撲巴戦の勝率 日本シリーズの勝敗確率 誕生日が一致する確率 誕生日が一致する確率(グラフ) 自分の誕生日と一致する確率 平均値と標準偏差から真の値を推計 サイコロの正確性 視聴率の誤差和の期待値 確率変数 が の サイコロの目の数が1,3のときに限り部屋を移る. また各試行の結果,部屋aに居る場合はその人の持ち点に1点を加え,部屋bに居る場合は1点を減らす. 持ち点は負になることもあるとする.3人で1回じゃんけんをするとき,勝者の人数の期待値を求めよ. 05 (人) 1 (人) 15 (人) 2 (人) 25 (人) 解説



期待値で根元事象で計算すると上手くいく問題 受験数学かずスクール



和の期待値
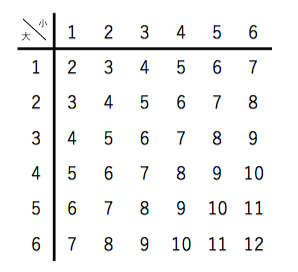
Apr 26, 10 · 7=(1,6)(2,5)(3,4)(4,3)(5,2)(6,1) 8=(2,6)(3,5)(4,4)(5,3)(6,2) 9=・・・ 10=・・・ 11=・・・ 12=(6,6) 求める期待値 =2*(1/36)3*(2/36)4*(3/36)・・・・11*(3/36)12*(1/36) =252/36=7 ※ 和の期待値=期待値の和 を知っていれば 1回サイコロを振ったときの期待値は7/2 なのでそれを2回行うので 7/2*2=7期待値の加法性 2確率変数の期待値と分散の性質(続き) 任意の確率変数X,Yに対し E(X+Y)=E(X)+E(Y) が成り立っている!(期待値の加法性) 例: Z n :サイコロをn回振ったときの目の和 とすれば, E(Z n )=n×E(Z 1 )=35n さらに一般に期待値の加法性 2確率変数の期待値と分散の性質(続き) 任意の確率変数X,Yに対し E(X+Y)=E(X)+E(Y) が成り立っている!(期待値の加法性) 例: Z n :サイコロをn回振ったときの目の和 とすれば, E(Z n )=n×E(Z 1 )=35n さらに一般に




数学a サイコロの最大値が5 最小値が2になる確率はどうやって考える 数スタ
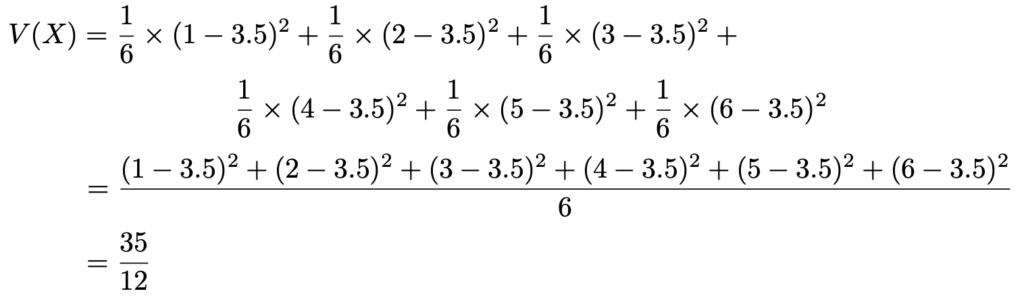



離散型確率変数の期待値と分散 中学の数学からはじめる統計検定2級講座第4回 とけたろうブログ
3 のときは続けたほうが賢明である.期待値は e(3) = 7 2 = 35 2 のときはやはり続けるべきである.期待値は e(2) = 6 6 5 6 4 6 7 12 2 6 1 6 = 43 12 »= 35¢¢¢ 1 のときも当然続けるべきで期待値は e(1) = 6 6 5 6 4 6 7 12 43 72 1 6 = 277 72 »= ¢¢¢Jan 13, 21 · 3個のサイコロの出目の和の期待値 = 3× (1個のサイコロの出目の和の期待値)Feb 19, 21 · 期待値が \(\displaystyle \frac{4}{3}\) であることから、サイコロを \(4\) 回投げて \(3\) の倍数が出る回数は「約 \(13\) 回」と期待できます。 もし \(3\) 回以上 \(3\) の倍数を出さなければいけない勝負をするとしたら、なかなか分の悪い勝負になりそうですね。




確率と統計 確率2回目 平成 18 年 11 月 1 日 2 今日の内容 1 確率の復習 再整理 2 加法の定理 3 乗法の定理へのイントロ Ppt Download



Excel De Asobo Section 6



ボードゲーム作りに絶対必要な確率の話 前編 やまだくうた ボードゲームの作り方 Note




和の期待値は期待値の和 高校数学の美しい物語



3個のサイコロを同時に投げるとき 出る目の数の和の平均を求めよ 解説 Yahoo 知恵袋



Probdistribution




期待値と分散の公式 証明と具体例 理数アラカルト



12 4 期待値の性質 統計学の時間 統計web




Studydoctor確率変数の和の期待値の求め方と公式 高校数学b Studydoctor




1 3 2 12 Lihat Cara Penyelesaian Di Qanda



二項分布とは 期待値 分散の計算や 正規分布による近似 受験辞典




期待値を計算するには 計算方法や公式をわかりやすく解説 高校生向け受験応援メディア 受験のミカタ




パッと見でわかる統計学ノート 分散や標準偏差において N 1 で割る公式の理由 アタリマエ




反復試行




さいころを2個同時に振ったとき 8なる確立 立方体のさいころを2個同 数学 教えて Goo



サイコロを50回振ったときに3の倍数の目が出る回数の期待値 分散 モードを Yahoo 知恵袋




期待値と分散の公式 証明と具体例 理数アラカルト




高校数学a 反復試行の確率 基本 Ncrp R 1 P N R 受験の月



期待値とは 計算公式と求め方 確率変数 確率分布の意味も 受験辞典



期待値とは 計算方法と具体例をわかりやすく解説 高校1年生向け ひよこseのつぶやきブログ




I B 35 2 Descubre Como Resolverlo En Qanda




確率の独立性の解説 積の期待値 和の分散 具体例 理数アラカルト



確率の基本 サイコロを投げる 苦手な数学を簡単に




授業実践記録



数学の授業 高校3年生数学b統計分野 での取り組みをご紹介します 筑波大学附属駒場中 高等学校 公式




第1章 場合の数と確率 第1節 場合の数 2 場合の数 第2回 Ppt Download




和の期待値は期待値の和 高校数学の美しい物語




確率の計算 サイコロを投げる場合 数学の偏差値を上げて合格を目指す



12 4 期待値の性質 統計学の時間 統計web




数学a サイコロの最大値が5 最小値が2になる確率はどうやって考える 数スタ




期待値と分散の公式 証明と具体例 理数アラカルト



確率は賭け事の理論




1 3 2 12 Lihat Cara Penyelesaian Di Qanda




株 日科技研 第24話 インドサイコロの確率計算 六一学者の千字一話 会員広場



サイコロを振り続けた時 目の和がある特定の値になる確率



確率を出してみた 串カツ田中のチンチロリンはやった方が得




期待値とは 確率変数の分散と標準偏差の求め方 Ax Bの期待値と分散 標準化 ますますmathが好きになる 魔法の数学ノート




りんだろぐ Rindalog 同時確率分布の期待値と分散の算出法



Probdistribution




期待値と分散の式が何故こうなるのか全く分かりません Clear



離散型確率変数の期待値と分散 中学の数学からはじめる統計検定2級講座第4回 とけたろうブログ




同時確率分布の期待値と分散の算出法 りんだろぐ Rindalog



期待値の計算法と意味 その使い方と注意点 アタリマエ



2個のさいころを同時に投げるとき 出る目の和の期待値を求めよ教え Yahoo 知恵袋




確率と統計 確率2回目 平成 18 年 11 月 1 日 2 今日の内容 1 確率の復習 再整理 2 加法の定理 3 乗法の定理へのイントロ Ppt Download




期待値と分散の式が何故こうなるのか全く分かりません Clear




数学 サイコロ なっちゃん




桃鉄 デストロイの出目が毎回期待値以上なんだが 桃鉄まとめ速報 桃太郎電鉄 昭和 平成 令和も定番




独立して失敗する人は期待値がわかってない 企業経営 会計 制度 東洋経済オンライン 経済ニュースの新基準



サイコロの目の平均 分散 標準偏差



サイコロを振り続けた時 目の和がある特定の値になる確率




サイコロ10コの出目の合計を当てろ やぐち建築士の備忘録



分散とは何か N個のデータと確率変数の分散の求め方について アタリマエ



期待値の質問です一個のサイコロを一回投げるとき 出る目の期待値を求めてくださ Yahoo 知恵袋




中心極限定理の意味 サイコロの具体例から分かる確率分布の正規近似 アタリマエ



Mondai71




期待値を計算するには 計算方法や公式をわかりやすく解説 高校生向け受験応援メディア 受験のミカタ




Abc194dの解答 Mo Note



素数とサイコロ




高校数学 数b 動画 確率変数の和と積 の問題 19ch




サイコロ3個を振った時の確立について質問です Okwave




期待値の意味と計算方法をコインやサイコロ ギャンブルゲームで考えてみる 統計学が わかった



相対する面の和が7である図1のサイコロ4個を互いに接する面の和が3又は9とな Yahoo 知恵袋



サイコロ10コの出目の合計を当てろ やぐち建築士の備忘録
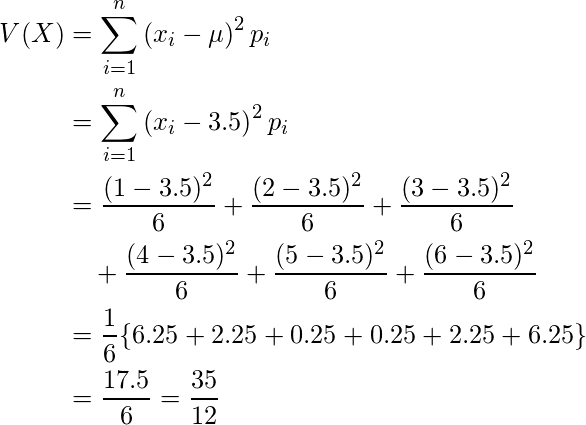



12 5 確率変数の分散 統計学の時間 統計web




平均値と期待値の違い 統計学が わかった




確率を出してみた 串カツ田中のチンチロリンはやった方が得



N個のサイコロの出目の和の場合の数にまつわる規則と その母関数 Togetter
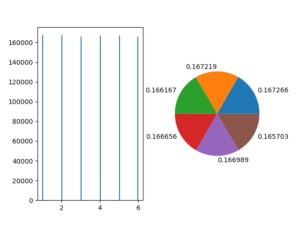



Python サイコロの目の期待値をプログラムで求めて確認してみた うたかたの高専生ブログ



首都大学東京 都市教養 文系 10年問題1 Suugaku Jp




確率の計算 サイコロを投げる場合 数学の偏差値を上げて合格を目指す




独立して失敗する人は期待値がわかってない 企業経営 会計 制度 東洋経済オンライン 経済ニュースの新基準



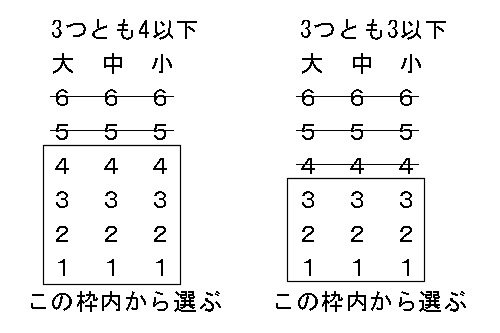
大中小3つのサイコロを投げたとき 3つの目の積が4以下になる場合の数を求めよ Yahoo 知恵袋




期待値とは 確率変数の分散と標準偏差の求め方 Ax Bの期待値と分散 標準化 ますますmathが好きになる 魔法の数学ノート



0 件のコメント:
コメントを投稿